Unbiased Learning-to-Rank with Biased Feedback

[usaito]

0. 論文概要

Thorsten Joachims, Adith Swaminathan, and Tobias Schnabel. 2017. Unbiased Learning-to-Rank with Biased Feedback. In Proc. of the 10th ACM International Conference on Web Search and Data Mining (WSDM). 781–789.

** 図表は基本的に本論文からの引用です. 一箇所だけ関連論文から引用しています.

1. 要約

• Implicit feedbackを使ったLearning-to-Rank (LTR) における新たなフレームワークとしてUnbiased Learning-to-Rankを提案.

• Implicit feedbackで得られるclickシグナルは真のrelevanceシグナルとは乖離しているためナイーブなloss functionはバイアスを持つ.

• 因果推論でよく用いられるIPSフレームワークを用いてloss functionを補正することで真のlossに対してunbiasedなlossを得ることができる. 実験では, ナイーブなlossを用いたRankSVMよりもIPSで補正したRankSVMの方が良い性能を示した.

2. 背景

• Implicit feedbackとしてclickシグナルを用いた既存のLTRには以下のlimitationsが存在.

1. clickをrelevanceと読み替えてlossを定義すると大きなbiasが生じてしまう
2. userがclickに至るまでの過程をモデル化し, その潜在変数を推定することでrelevanceシグナルを推定するアプローチのclick modelは, 同じqueryのログが複数回記録されている必要があり, 時として非現実的.
3. ランダムなランキング表示によって得られたclickシグナルはrelevanceシグナルと読み替えてもbiasは生じないが, ランダムランキングで十分なデータを蓄積するのは大きなコスト.

したがって, ランダムなランキングを表示することでデータを集めるという過程を必要とせずとも, できるだけ真のrelevanceに対して最適化できるようなloss functionを得たいよね, というモチベーションが生まれる.

3. 手法

IPSアプローチに入る前にfull-information のLTRの定式化を確認する. Xはiidで得られるquery sample, rel(x, y)はquery xとdocument yのrelevanceシグナル, \Delta(\vec{y} | x)をquery xに対してdocumentのランキング\vec{y} を提示した時のlossとする. この時, ranking function Sに対する真のlossは以下のように定義される. もちろん真のquery分布はわからないため, 実際に最適化するのはデータから計算される経験loss.

しかし, 今考えている系は部分的にしか情報を得ることができない系である. これをモデル化するために, relevanceが観測されるか否かを表すbinary確率変数Oを導入する. この時, Qをpropensityスコアとする.

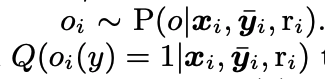
このpropensityスコアの逆数で重みつけして計算されるlossは真のlossに対してunbiasedであることが以下のように示される.

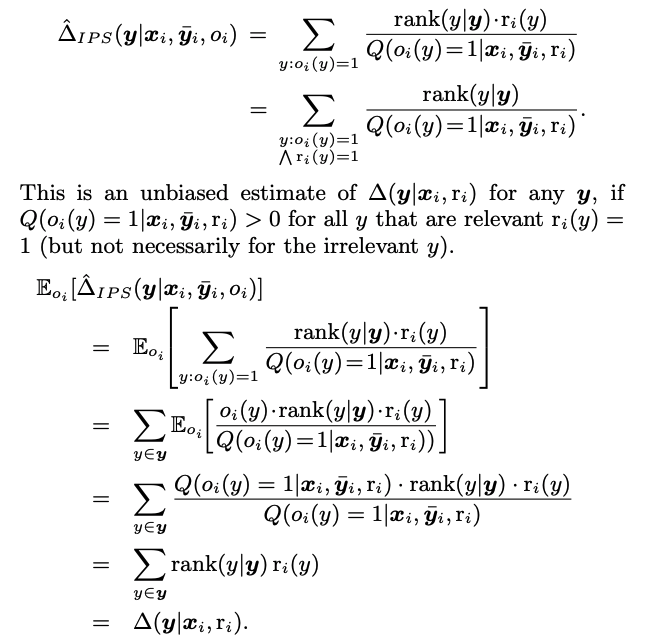
よって, このIPSによるlossをデータから推定した経験lossも真のlossに対してunbiasedである. よって, これを最小化すればbiasは生まれず, 学習データが増えるにつれrelevanceに対して真に最適なranking functionに収束していくと考えられる.

IPSを用いるとbiasを除去できることがわかったが, どうやってpropensityを推定すれば良いのだろうか？ ここで本論文はpropensityを推定するために, click propensity modelというモデル化を導入する. ここでは新たにeで表されるexaminedシグナルが登場する.

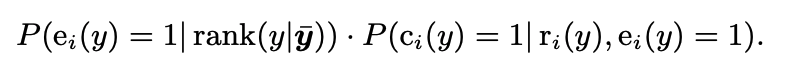
つまり, clickが発生する確率は, あるqueryに対してdocumentが（表示されたpositionにおいて）認知される確率と, relevanceに依存したclickされる条件付き確率の積に等しいというモデル. ここで, 本論文では, c=1とe=1かつr=1は同値であるという仮定を置く. つまり, クリックが発生するのは認知されたかつrelevantであることが必要かつそのときのみである. この仮定によりeとoが同値であることが言えるので, propensityを求めるためには, 各表示positionに依存する認知確率を推定すれば良いことになる.

これは（小規模の）result randomizationによって求めることができる. Top N positionの表示をランダムにすると, propensityとクリック確率が比例するというもの. 実は, IPSでは各positionのpropensityの比がわかっていれば十分なので, 比例する値が求まれば良い.

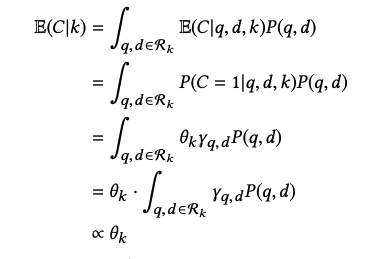
** この図のみ関連論文からの引用です.

ここで, propensity推定のために置いたpropensity modelの仮定が非現実的だよねという話に入る. よってより現実的な以下のclick noiseを許容することを考える. つまり, relevantなdocumentでも幾らかの確率でスルーしてしまうし, 非relevantなdocumentも幾らかの確率で誤clickしてしまうということ.

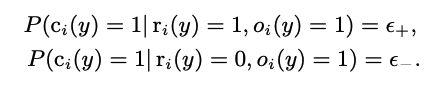
実は, このようなclick noiseを導入しても, IPSによる経験lossの期待値の順位は真のlossの順位と一致することが示される. のでclick noiseが存在していたとしても, IPSによるlossは正当性を持つ.

以上長々とIPSアプローチについて記述してきたが, 本論文の提案アルゴリズムはSVM-Rankのlossをpropensityで重みつけしたPropensity SVM-Rankである.

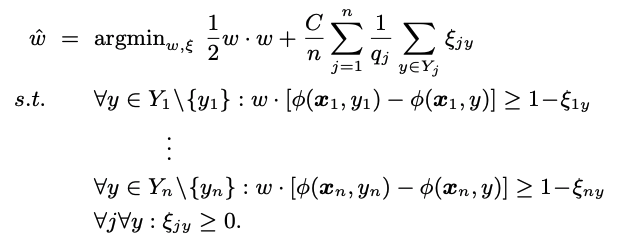
4. 実験

• 真のpropensityを自ら生成する人工データを使った実験.

1. トレーニングデータのサイズが大きくなった時の性能の推移

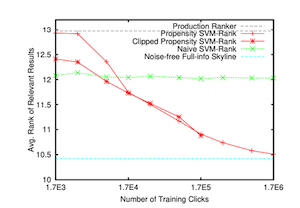
2. positionによってpropensityが大きく変化する際の性能の推移

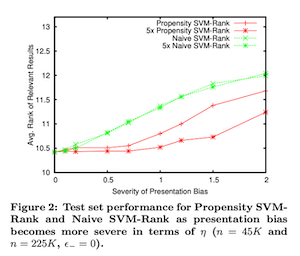
3. click noiseの大きさが変化した時の性能の推移

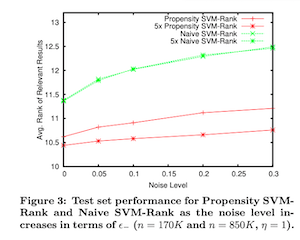
トレーニングデータが極小の場合はIPSによるvariance増大の影響が出るため提案手法がnaive SVM-Rankに負けるがそれ以外の設定では基本naive手法を上回っており, IPSアプローチが効果的であることを示す. 特にトレーニングデータが増えた時は, noise-free full-infoで学習した最適に近いSVM-Rankに近い性能を見せた. しかし注意点として, これらの結果は真のpropensityを使ったpropensity SVM-Rankによるものであるということである.

4. propensityの推定誤差が変化した時の推定誤差.

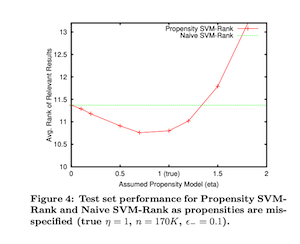
実際は, propensityを推定しなければならない. よってpropensityに推定誤差が存在する時の性能の変化を調べたのがこのグラフ. これを見ると大きな推定誤差が生まれる時以外は, naive SVM-Rankを上回る性能を示していることがわかるので, propensityの誤推定に対してもある程度頑健だという主張がなされている.

5. コメント

• Implicit FeedbackのLTRに対しIPSアプローチを適用できることを示した点が最も大きな貢献だろう. 2018年現在多くの後続研究がなされており, Unbiased LTRは１つの研究分野として確立した感がある.

• 一方で, propensity推定のためにresult randomizationが必要というのは大きな制約だと思われる. 彼らはresult randomizationは小規模で良いと書いているが実際のところは不明である. この問題を解決しようとしたのが関連論文にピックアップした論文で, logデータからpropensityを推定する方法を提案している.

6. 関連論文ピックアップ

• Xuanhui Wang, Nadav Golbandi, Michael Bendersky, Donald Metzler, Marc Najork. 2018. Position Bias Estimation for Unbiased Learning to Rank in Personal Search. In WSDM 2018: WSDM 2018: The Eleventh ACM International Conference on Web Search and Data Mining , February 5–9, 2018, Marina Del Rey, CA, USA. ACM, New York, NY, USA