Elliptic.jl
Elliptic.jl copied to clipboard
Published
3 years ago
•
nolta
nolta
Elliptic integral and Jacobi elliptic special functions
Elliptic Special Functions for Julia
This julia package implements
elliptic integrals and
(in the Jacobi sub-module) the
Jacobi elliptic functions.
Elliptic Integrals
| Function | Definition |
|---|---|
F(phi, m) |
Incomplete elliptic integral of the first kind, F(φ | m) |
K(m) |
Complete elliptic integral of the first kind, the quarter period, F(π/2 | m) |
E(phi, m) |
Incomplete elliptic integral of the second kind, E(φ | m) |
E(m) |
Complete elliptic integral of the second kind, E(π/2 | m) |
Pi(n, phi, m) Π(n, phi, m) |
Incomplete elliptic integral of the third kind, Π(n; φ | m) |
Where the parameter m = k^2 = sin(α)^2, α is the modular angle, k is the modulus, and
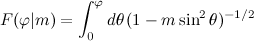
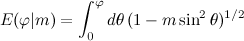
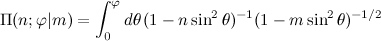
julia> import Elliptic
julia> Elliptic.K(0.5)
1.854074677301372
Jacobi Elliptic Functions
| Function | Definition |
|---|---|
am(u, m) |
Solution to u = F(am(u | m) | m) |
sn(u, m) |
sn(u | m) = sin(am(u | m)) |
cn(u, m) |
cn(u | m) = cos(am(u | m)) |
dn(u, m) |
dn(u | m) = sqrt(1 - m sn(u | m)^2) |
sd(u, m) |
sd(u | m) = sn(u | m) / dn(u | m) |
cd(u, m) |
cd(u | m) = cn(u | m) / dn(u | m) |
nd(u, m) |
nd(u | m) = 1 / dn(u | m) |
dc(u, m) |
dc(u | m) = 1 / cd(u | n) |
nc(u, m) |
nc(u | m) = 1 / cn(u | m) |
sc(u, m) |
sc(u | m) = sn(u | m) / cn(u | m) |
ns(u, m) |
ns(u | m) = 1 / sn(u | m) |
ds(u, m) |
ds(u | m) = 1 / sd(u | m) |
cs(u, m) |
cs(u | m) = 1 / sc(u | m) |
julia> import Elliptic.Jacobi
julia> Jacobi.sn(2, 9)
-0.15028246569211734
Matlab Compatibility
| Function | Definition |
|---|---|
ellipj(u, m) |
returns (sn(u,m), cn(u,m), dn(u,m)) |
ellipke(m) |
returns (K(m), E(m)) |
For convenience, the matlab compatible ellipj and ellipke routines are
also provided. ellipj(u,m) is equivalent to sn(u,m), cn(u,m), dn(u,m),
but faster if you want all three. Likewise, ellipke(m) is equivalent to
K(m), E(m), but faster if you want both.
julia> import Elliptic
julia> k,e = Elliptic.ellipke(0.5)
(1.854074677301372,1.3506438810476757)
julia> sn,cn,dn = Elliptic.ellipj(0.672, 0.36)
(0.6095196917919022,0.792770928653356,0.9307281387786907)
Installation
julia> Pkg.add("Elliptic")
nolta