union/intersection modes like in the R version
This is such a great package! Thanks. I noticed that in the R version of the code there are 4 modes for how to compute the intersections, described here: https://krassowski.github.io/complex-upset/articles/Examples_Python.html#0-2-region-selection-modes
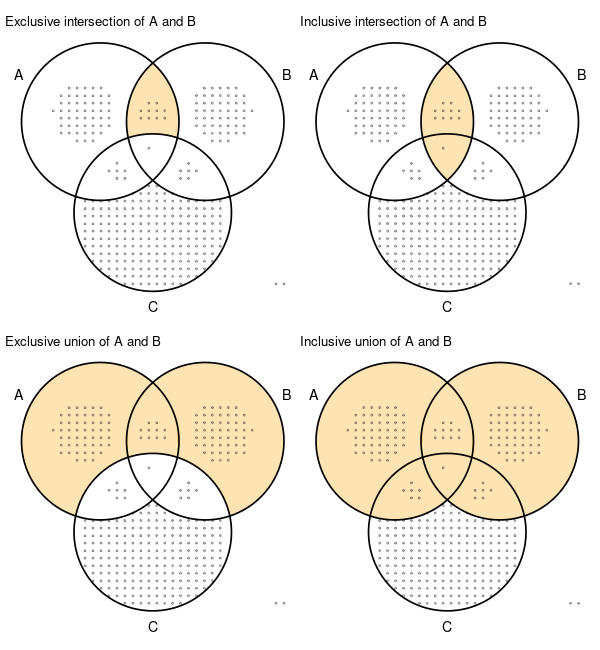
I was wondering if there was a way to do this directly in python.
Thanks, Adam
Thanks for your interest and praise!
This is not currently supported. A quick-to-implement but not-optimally-efficient solution would involve reduplicating data elements to handle attribute plots (e.g. add_catplot)...
We would replace the _bin assignment logic here:
https://github.com/jnothman/UpSetPlot/blob/14e5425eec78ccb10ac7803f129463681ee0139c/upsetplot/plotting.py#L29-L48
Instead we would build a mapping from boolean set indicators to bin number that incorporates a "region of interest" parameter.
Then we would pd.merge data and agg with this mapping, and sum over _bin in agg.
We would also want to update the default ylabel, i.e. "intersection size".
If you'd like to have a go implementing it, please feel free to do so!
thanks! I'll have a go at it soon, and will post here if I get something working.
I've made a function which maps from a boolean set indicator to a set of boolean set indicators, in order to map e.g. [ [True, True, False], [True, True, True] ], ie. from the exclusive intersection set to the inclusive intersection set, which is a set of exclusive intersection sets.
My thinking is that we could go through every multi-index in agg and sum up all values at the multi-index values that the mapping gives you. Unfortunately I'm not that great at coding/pandas and I'm a bit stuck. I don't want to waste your time but I was wondering if you could point me in the right direction, if it's not too much help.
I was going to iterate through every multi-index value in agg, and then replace the value with the sum of all the agg rows that my new function tells me. This would be enough to create the graph I wanted. Unfortunately I can't even figure out how to iterate through the multiindex.
Here is the function I wrote
def get_inclusive_intersections(vec):
"""
This function maps an exclusive intersection to an inclusive intersection
and presents that inclusive intersection as a set of exclusive
intersections. These exclusive intersections are represented as booleans.
E.g. [True, True, False] means the exclusive intersection between
sets A and B, and this should map to the set:
[ [True, True, False], [True, True, True] ]
Parameters
----------
vec : list
a boolean list.
Returns
-------
l2 : list of boolean lists
DESCRIPTION.
"""
import itertools
bools = [True, False]
# Compute the number of False elements there are, and the locations
# of all True. We want to permute over all False locations, so we
# make all boolean permutations length-Falses long, and then insert
# in the Trues where they belong.
reps = vec.count(False)
locs = np.where(np.array(vec)==True)[0]
l = [list(i) for i in itertools.product(bools, repeat=reps)]
l2 = [np.insert(x, locs ,True) for x in l]
return l2
Thanks! We want to find all sets of exclusive intersections that compose some inclusive intersection / exclusive union / inclusive union.
I would probably do this with bit vector representations as produced by _pack_binary above. Then [ [True, True, False], [True, True, True] ] maps to [6, 7]. We can use bitwise ops over all pairs of intersections to map 6 to [6,7] by comparing each query bit vector to each other bit vector. Then we can use conditions like:
- inclusive intersection:
query & other == query - inclusive union:
query | other == other
But the right way to develop this is to write some tests first for building the mapping.
Writing a test first makes me think there are many ways to do this :)
def expand_regions(n_sets, mode="exclusive-intersection"):
"""
Parameters
----------
n_sets : int
mode : {"intersection", "inclusive-intersection", "exclusive-union", "union"}
Returns
-------
dict
a mapping from masks of length n_sets to a collection of its constituent intersection masks
"""
...
@pytest.mark.parametrize('mode,expected', [
("intersection", {
(0, 0): {(0, 0)},
(1, 0): {(1, 0)},
(1, 1): {(1, 1)},
}),
("inclusive-intersection", {
(0, 0): {(0, 0)},
(1, 0): {(1, 0)},
(1, 1): {(1, 0), (0, 1), (1, 1)},
}),
("exclusive-union", {
(0, 0): {(0, 0)},
(1, 0): {(1, 0)},
(1, 1): {(1, 0), (0, 1),},
}),
("union", {
(0, 0): {(0, 0)},
(1, 0): {(1, 0)},
(1, 1): {(1, 0), (0, 1), (1, 1)},
}),
("inclusive-intersection", {
(0, 0, 0): {(0, 0, 0)},
(1, 0, 0): {(1, 0, 0),},
(1, 1, 0): {(1, 0, 0), (1, 1, 0), (0, 1, 0)},
(1, 1, 1): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 0), (0, 1, 1), (1, 1, 1)},
}),
("exclusive-union", {
(0, 0, 0): {(0, 0, 0)},
(1, 0, 0): {(1, 0, 0),},
(1, 1, 0): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 0), (0, 1, 1)},
(1, 1, 1): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 0), (0, 1, 1), (1, 1, 1)},
}),
("union", {
(0, 0, 0): {(0, 0, 0)},
(1, 0, 0): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1)},
(1, 1, 0): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 0), (0, 1, 1)},
(1, 1, 1): {(1, 0, 0), (1, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 0), (0, 1, 1), (1, 1, 1)},
}),
])
def test_expand_regions_examples(mode, expected):
n_sets = len(next(iter(expected.values())))
actual = expand_regions(n_sets, mode)
def mask_to_01(a):
return tuple(a.astype(int))
actual = {mask_to_01(k): set(map(mask_to_01, v)) for k, v in actual.items()}
# limit to the example keys
actual = {k: v for k, v in actual.items() if k in expected}
assert actual == expected
@pytest.mark.parametrize('n_sets', [1, 2, 3, 4])
@pytest.mark.parametrize('mode', ["intersection", "inclusive-intersection", "exclusive-union", "union"])
def test_expand_regions_permutation_invariance(n_sets, mode):
# TODO: assert that a permutation of the input columns produces the corresponding outputs
pytest.skip()
While I recognise this is a popular request, I have considered this feature request, and I would rather not introduce this level of complexity to:
- the meaning of the basic upset plot
- the code maintenance
Supporting different kinds of set relationship could indeed be useful, and makes most sense in an interactive data exploration tool like those listed at https://upset.app/implementations/. However, there is a simplicity to the current plot, where each data point is represented exactly once (if not filtered out).
As such, I'm resolving not to implement this request.