jeffThompson
small Explanation mistakes
Hi, first: I really like your project and enjoyed reading it and please excuse my englisch I'm no native english speaker.
I got very enthusiastic about trying out your code and analyze your explanations. And found one slight mistakes and want to give you a hint for the Point / Polygon code:
http://www.jeffreythompson.org/collision-detection/line-circle.php
Then, we get a value we’re calling dot. If you’ve done vector math before, this is the same as doing the dot product of two vectors. If this isn’t familiar, no worry! Consider this step a lot of math you can be glad not to have to solve by hand:
Actually it isn't the dot product. It is a scalar projection (or scalar component) of the vector P1->CircleCenter onto the vector P1->P2. If you want to explain this further :
The dot product of two vectors a and b equals the magnitude of both times the cosine of the angle between them.
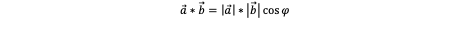You can also find further information here (or link it on your website :) : https://en.wikipedia.org/wiki/Dot_product#Scalar_projection_and_first_properties
For my own project I thought a long time about the shorthand algorithm behind the vertices line segment intersection (http://www.jeffreythompson.org/collision-detection/poly-point.php)
px < (vn.x-vc.x) * (py-vc.y) / (vn.y-vc.y) + vc.x
The Basic Jordan Curve Theorem is working as follows: You choose a point out of the polygon and send a ray in an arbitrary direction. In your code its the direction of the x-axis (This is given by your first boolean check which you explained very well on your website). Then you test how many intersections with the edges (line segments) of the polygon you have. Therefor you need the current and next Vertex to build a line segment.
I found a decent explanation for the second boolean test after some try and failure:
The magic happens in finding an equation for the line segment and a bit of sorting for better readability.
Everyone knows the equation for the y value of a line segment from school:
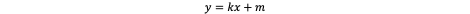A line segment's x value is given with the equation:
with k as the slope of the segment:
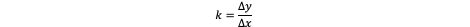Therefore you get the following equation:
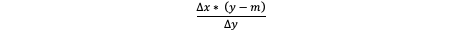
The given Y you want the X value for is the point's y coordinate. In your code m is vc.y therefore the line segments intersects the y axis at the y value of vc which looks something like:
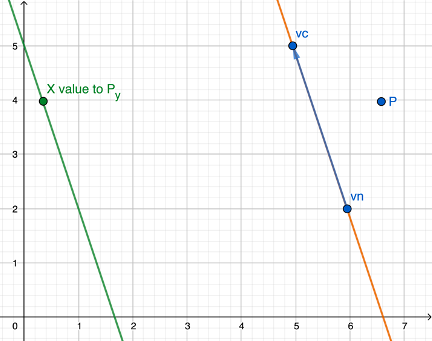
now you have the equation px < (vn.x-vc.x) * (py-vc.y) / (vn.y-vc.y) and the visualization for the line segment of the Polygon (blue) and the equation (green).
The last thing missing is the back transformation to the real coordinates. This happens with adding vc.x.
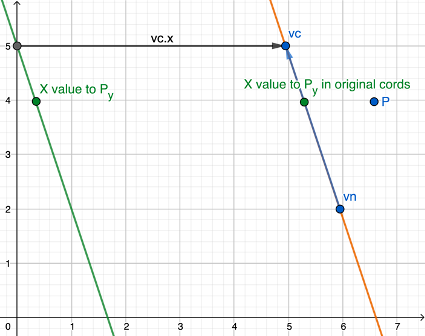
When your computed x coordinate is smaller than your point's x ... ...then the Point is not "intersecting" (okay a point can't actually intersect but i hope you know what i want to say) When your computed x coordinate is bigger than your point's x ... ... you can assume an intersection of the Point.
This is names semi-infinite Ray-casting... because as long as your polygon is "existing" the ray extends, but it stops when the polygon does.
This got longer than i expected, but i hope it helps as you mentioned on your website:
(If you understand how this algorithm works, please do let me know!)
