imuncle
四足机器人制作（一） 腿部运动算法
前段时间MIT的新型迷你猎豹机器人火遍全网，当时我就心里痒痒要做一个，但是正在备赛RM就没做，后来看到祁乐老哥做了一个舵机4足机器人（看这里），更是刺激了我，现在终于比赛结束了（sad :cry:），准备动手研究四足机器人。
我也打算做一个带12个舵机的四足机器人，一是这种类型的四足比较像一个四足，是我最喜欢的一种形态，二是穷，买不起好电机。
这是一系列制作过程记录，也可以把它当做教程吧，不定期更新，我也不知道什么时候能做出来，毕竟现在一穷二白，电机都买不起，还正值期末考试。
那么正式开始了，首先是腿部算法。
腿部简介
首先还是看一看机器人的腿部结构吧，这里直接借用祁乐老哥的机器人一用
从上图可以看出，每一个腿部有三个自由度，所以对应的我们每次更新机器人姿态时都要计算出这三个舵机的角度。
首先看看两个自由度下，腿部的在平面内运动的情况。
腿部平面运动
可以将模型抽象如下
我们的目标转变为根据C点坐标计算α和β角度，这里其实就是解三角函数。上图中的直线a和b就是机器人的两条腿，是可以直接测量出来的。
首先用勾股定理求出直线c的长度，然后在△ABC中运用余弦定理，可计算出∠β和∠BAC，进而求出∠α
最后求出的结果如下
上述公式中要注意的就是坐标系的正方向的选取，也就是x和y的正负号问题。
根据上述公式就可以把二维平面的坐标转换为两个舵机的角度，进而转换为舵机的控制信号。当然要还要注意C点的取值范围，毕竟腿长是有限的。
腿部三维运动
现在把腿放在三维空间中看看，可以把模型简化如下
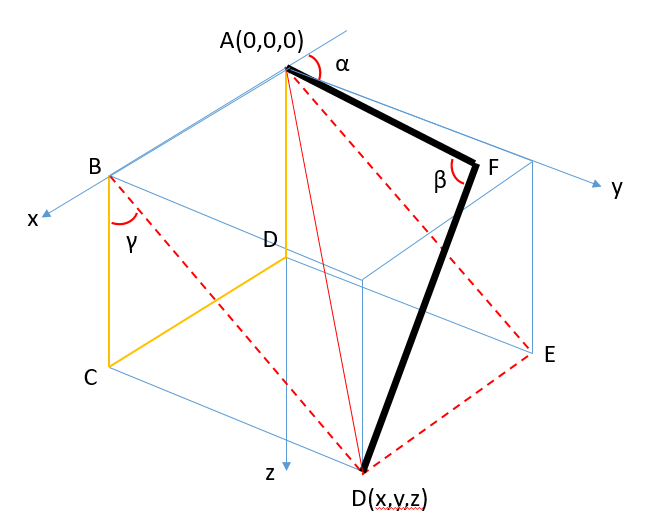
上图中黑色的两条线代表腿部的大腿和小腿两段，α、β和γ分别代表腿部三个舵机的角度位置。
面ABCD是机器人直立时腿部所在平面，即面ABCD垂直于地面。
很容易看出，腿部一定在面ABDE中，那么∠α和∠β就可以在面ABDE中，在二维平面内，用上述的方法求解出。∠γ可以在△BCD中求解出来。
最后求出的结果如下：
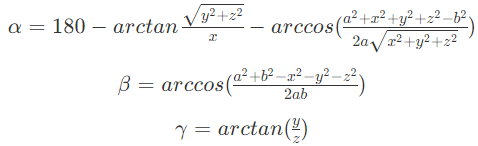
下期预告
至此，单条腿部的运动就完成了，将上述方程封装成函数，只需要指定目标点的坐标就可以了。
接下来要做的是如何协调四条腿控制四足机器人的姿态，即四足机器人的姿态解析。这个就留在下一篇文章写吧，也挺简单的。
参考
最近在研究这个四足机器人，网上博文太杂，发现您这个写的很不错，跟我的思路一样，由于图片看不到，一些图片分析都理解不到，能把这几篇文章发到邮箱吗？非常感谢！！！！！[email protected]
---原始邮件--- 发件人: "big_uncle"<[email protected]> 发送时间: 2020年12月12日(周六) 上午10:06 收件人: "imuncle/imuncle.github.io"<[email protected]>; 抄送: "Mention"<[email protected]>;"半盏清酒"<[email protected]>; 主题: Re: [imuncle/imuncle.github.io] 四足机器人制作（一） 腿部运动算法 (#61)
图片看不到
@LSC123 没办法，最近GitHub的raw.githubusercontent.com被墙的厉害
— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub, or unsubscribe.