Adding user biases and item biases for implicit matrix factorization

[SimonCW]

Hi @benfred ,

I was wondering whether adding user and item biases would improve the model and recommendations. Did you consider this at some point or experiment with it? Would you expect better performance?

Intuitively, I fear that without biases very popular items will dominate the recommendations more strongly than I want.

Literature:

• The original paper only talks about biases in the context of item-based neighbourhood models (section 3.1 in http://yifanhu.net/PUB/cf.pdf) but not in the context of the objective function.
• There is this (somewhat obscure) article which claims that performance is better with biases: http://activisiongamescience.github.io/2016/01/11/Implicit-Recommender-Systems-Biased-Matrix-Factorization/
• Well, most implementations of implicit matrix factorization (e.g. Spark) don't use biases.

Would love to hear your take on it! Best Simon

[FCHal]

Hi Ben and Simon,

I was wondering the same thing. Therefore I am writing the comment to be able to follow the conversation easily. I found a MF implementation that includes the biases at http://www.albertauyeung.com/post/python-matrix-factorization/ Where num_users and num_items correspond to the shape of the matrix, and R is the user-item rating matrix. I remain unsure on how and where to implement this into the existing implicit package.

    # Initialize the biases
    self.b_u = np.zeros(self.num_users)
    self.b_i = np.zeros(self.num_items)
    self.b = np.mean(self.R[np.where(self.R != 0)])

Kind regards,

Floris

[ghost]

@benfred and @ita9naiwa ,

I am also trying to add biases into the model, as described by: http://activisiongamescience.github.io/2016/01/11/Implicit-Recommender-Systems-Biased-Matrix-Factorization/

I want to add the following steps during fitting of the model:

I have been going through the source code of the package, but unfortunately my python and cython skills are not sufficient to address the issue. I am using an AlternatingLeastSquares model with native extensions (use_native=True), but without Conjugate Gradient (use_cg = False). Is there any way to implement these biases into the model?

Already a great package by the way!

Kind regards,

Maarten

[ita9naiwa]

we can implement bias by fixing the last element of the user factors to be 1, and last - 1 element of the item factors to be 1

as LMF implemented. https://github.com/benfred/implicit/blob/fbed6211547e676ba414fdf734432aa3252ac90b/implicit/lmf.pyx#L169-L181

but I'm not sure adding bias will be a good idea.

It would be very nice to compare the performance of WMF with and without bias terms.

[lethaiq]

@ita9naiwa thanks for the comment. Why the index of the user_factors is -2 and that of item_factors is -1? Isn't it need to be both -1 (last element index)? I am not sure what I am missing here.

[ghost]

@ita9naiwa , thanks for your response! I will try to implement it in the coming week.

Is there by the way any reason to assume that the bias would not improve the results, rather than the fact that it is not mentioned by the original paper of Hu, Koren and Volinksy? I am currently writing a thesis about the topic and my professor thinks it would be better to include biases. At the same time I do realize that a lot of the bias is already removed by converting actual purchase frequencies into the confidence (weighting) and preference mapping. But I still think it can do no harm to add the biases. Curious to hear your opinion on the matter!

[lethaiq]

@Maartenraaij I am curious that when you factor the purchase frequencies into confidence (weighting), which I assume the C matrix in the original paper loss function, did you get a better results compared with setting C uniformly? And may I ask what is preference mapping here?

[ghost]

With preference mapping I meant the transformation from the implicit feedback ratings into the preference variable. So say a person bought item 'i' 5 times, it's preference will be 1, while the preference is 0 for every item not bought.

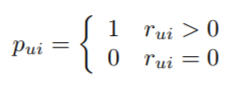
What do you mean with setting C uniformly? I follow the original paper and set them 'uniformly' in the sense that the confidence increases equally over the purchase frequency. But setting C 'uniformly' in the sense that it is equal for every item would defeat it's purpose.

[lethaiq]

@Maartenraaij oh thanks. Sorry the word uniformly is not correctly used. I guess the context of your problem is little bit different, but I would love to have the bias incorporated into the library as well.

@ita9naiwa can you briefly show us how to add bias term?

[ita9naiwa]

let u = [x_1, x_2, ..., x_n] and i = [y_1, y_2, ..., y_n]

We define u' = [x_1, x_2, ..., x_n, 1, u_b], i' = [y_1, y_2, ... y_n, i_b, 1]

dot product between u' and i' gives

    dot(u', i') = 
    =  x_1 * y_1 + ..., x_n * y_n + 1 * i_b + 1 * u_b
    = (x_1 * y_1 + x_2 *y_2 + ... x_n * y_n) + i_b + u_b
    =  dot(u, i) + i_b + u_b

The implementation of BPR and LMF exploits the same property.

updating factors using gradient descent goes similarly.

[ita9naiwa]

I'm not sure adding bias terms is a good idea because we can't interpret cosine similarity between items,(or users) anymore if we add bias terms.

Therefore, in my opinion, I will not add the bias terms for users and items unless there is a performance gain for sure and in case it added, it must be optional.

[howtodowtle]

I'm not sure adding bias terms is a good idea because we can't interpret cosine similarity between items,(or users) anymore if we add bias terms.

@ita9naiwa

Couldn't we just compare the user/item factors without their bias terms (and the fixed 1s)?

def debias(factors):
    return factors[:, :-2]

self.uf_no_bias, self.if_no_bias = map(debias, (self.user_factors, self.item_factors))

Then compare items or users as before, just now pulling the vectors out of self.if_no_bias/self.uf_no_bias instead of self.user_factors/self.item_factors. (Edit: Or pulling from the original matrices and removing the bias term on the go.)

(Edit: Just noticed I had a mistake in the code and it's even simpler than I thought.)

[howtodowtle]

https://github.com/benfred/implicit/blob/fbed6211547e676ba414fdf734432aa3252ac90b/implicit/lmf.pyx#L169-L181

Very clever way of implementing the bias terms, by the way. :)

[guyba-tr]

I'm not sure adding bias terms is a good idea because we can't interpret cosine similarity between items,(or users) anymore if we add bias terms.

Therefore, in my opinion, I will not add the bias terms for users and items unless there is a performance gain for sure and in case it added, it must be optional.

@ita9naiwa Is the only drawback the interpretation? or can it also damage performance?

I too am eagerly waiting for this addition to the code..

[howtodowtle]

I'm not sure adding bias terms is a good idea because we can't interpret cosine similarity between items,(or users) anymore if we add bias terms. Therefore, in my opinion, I will not add the bias terms for users and items unless there is a performance gain for sure and in case it added, it must be optional.

@ita9naiwa Is the only drawback the interpretation? or can it also damage performance?

I too am eagerly waiting for this addition to the code..

1. The interpretation is not a drawback if you remove the bias terms before comparison.
2. ~~It should improve performance.~~ (Actually I'm not sure if there's a consensus on that.)
3. The code is already there in this discussion. ;) I might make a MR/PR though if I get to it. (edit: I did.)

[julioasotodv]

An alternative to having the model learn user and item biases is to just modify the input matrix in ALS to account for those biases (a simple way is just to subtract the mean rating for a user from all the user's ratings; or doing it the other way around item-wise).

This way you should be able to normalize ratings user-wise or item-wise. If you want to do both, you can just estimate both biases using least squares for instance (linear regression).

I am not sure whether adding bias terms to the model is worth it, as it makes everything more complicated. Especially given that the PR #310 has been open for a year and a half... Maybe it is just better to show how to do it externally (as I described above) and make that clear in the docs?