Poly chaos

[FHoltorf]

Hey,

I need #8 going forward and so I prepared a first draft. Specifically, this implementation addresses the generation of moment equations for polynomial models via Galerkin projection. Extending it for non-polynomial terms is left for future work as non-polynomial terms need to be handled approximately and accordingly there are many different approaches to do that approximation. Any polynomial basis as supported by PolyChaos.jl is supported. That means that a large subset of polynomials from the Askey scheme and some additional useful ones are available (including polynomials wrt user-defined weighting/density functions). That said, it also means that currently only dense polynomial bases with equal degree in all dimensions are supported. While that wouldn't be strictly necessary and this implementation could be adjusted for more liberty in that regard, it is not natural with the way PolyChaos.jl is constructed and I think we should change PolyChaos.jl itself to accommodate sparse polynomial bases. That change would probably be less involved. The generalization would then carry over automatically.

I will add a tutorial style example to showcase potential usage soon.

Flemming

[codecov[bot]]

Codecov Report

Merging #27 (f6931d4) into main (d1fc6ac) will decrease coverage by 4.12%. The diff coverage is 85.65%.

@@            Coverage Diff             @@
##             main      #27      +/-   ##
==========================================
- Coverage   92.96%   88.84%   -4.13%     
==========================================
  Files           5        7       +2     
  Lines         199      457     +258     
==========================================
+ Hits          185      406     +221     
- Misses         14       51      +37     

Impacted Files	Coverage Δ
src/DEIM/deim.jl	100.00% <ø> (ø)
src/DEIM/utils.jl	100.00% <ø> (ø)
src/PCE/PCE_utils.jl	80.48% <80.48%> (ø)
src/PCE/PCE.jl	94.68% <94.68%> (ø)

:mega: We’re building smart automated test selection to slash your CI/CD build times. Learn more

[FHoltorf]

A Brief Update

The current state of the draft appears to be working quite well and in my opinion already provides some useful functionality. Below you can see an example for generating and solving the PCE moment equations for a reaction system with uncertain rate coefficients.

# Reaction system
# k[1](1+θ[1]/2)/k[2]: A + B ⇌ C 
# k[3](1+θ[2]/2):      C → D
# k[4]:                B → D
# 
# state: c[1:4] = [A, B, C, D]
# certain parameters: k[1:4]
# uncertain parameters: θ[1:2] ∼ U[-1,1] 

@parameters k[1:4], θ[1:2]
@variables t, c(t)[1:4]
D = Differential(t)
reactor = [D(c[1]) ~ -k[1] * (1 + 0.5 * θ[1]) * c[1] * c[2] + k[2] * c[3];
           D(c[2]) ~ -k[1] * (1 + 0.5 * θ[1]) * c[1] * c[2] - k[4] * c[2] + k[2] * c[3];
           D(c[3]) ~ k[1] * c[1] * c[2] - k[3] * c[3];
           D(c[4]) ~ k[3] * (1 + 0.5 * θ[2]) * c[3] + k[4] * c[2]];

@named reactor_model = ODESystem(reactor, t, c, vcat(k, θ))

# 1. choose/generate PCE of the system state
d_pce = 3
pce = PCE(c, [θ[i] => Uniform_11OrthoPoly(d_pce) for i in eachindex(θ)])

# 2. generate moment equations
moment_eqs, pce_eval = moment_equations(reactor_model, pce)

# 3. solve the moment equations
# 3a. find initial moments via Galerkin projection (note that c0 could depend on an uncertain parameter)
c0 = [1.0, 2.0, 0.0, 0.0]
z0 = reduce(vcat, pce_galerkin(c0, pce))

# 3b. solve the initial value problem for the moment equations
moment_prob = ODEProblem(moment_eqs, z0, (0.0, 10.0),
                         [k[1] => 1.0, k[2] => 0.2, k[3] => 12, k[4] => 0.1])
moment_sol = solve(moment_prob, Tsit5())

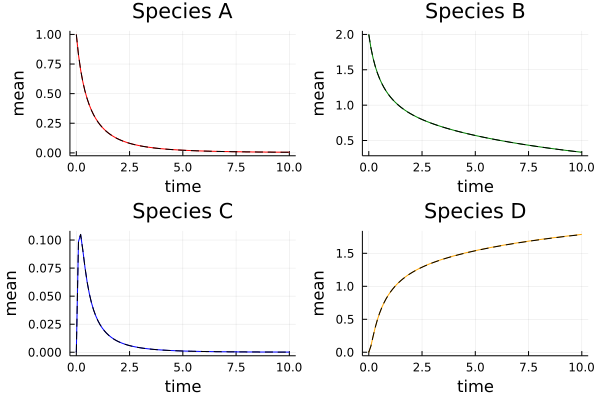
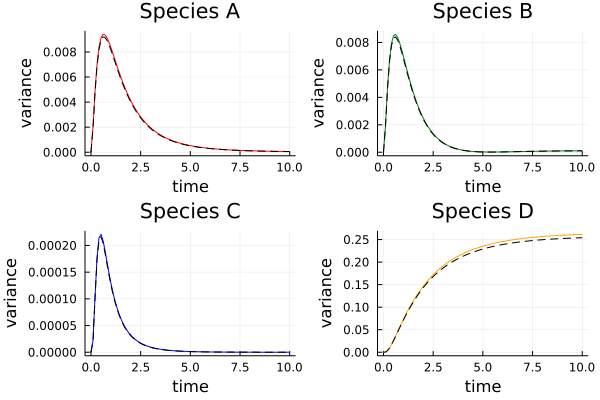
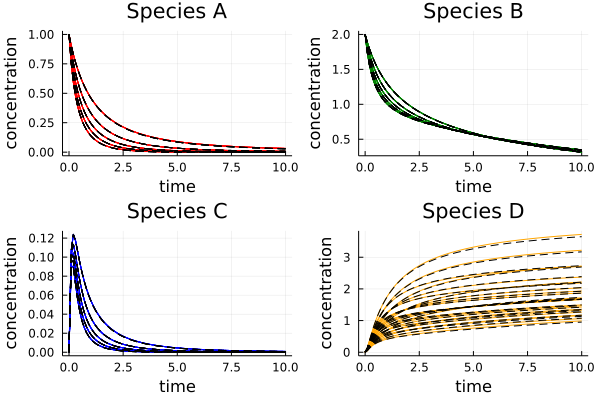
The results appear consistent as well. The figures below show a comparison between sampling (solid colored lines) and PCE (dashed black lines) results.

comparison of mean prediction

comparison of variance prediction

comparison of traces for various parametric realizations

More details can be found here.

Let me know if you have any thoughts on how to proceed from here.

[FHoltorf]

Hey, any thoughts on this @ChrisRackauckas @bowenszhu? The basic functionality of generating PCE moment equations works quite nicely and robustly for polynomial explicit ODE models (see example above). In the future, it would be good to explore the following extensions (importance vaguely in descending order):

• Support for PDE models (integration with MethodOfLines.jl) -> PCE moment equations generated from discretized models vs. discretization of PCE moment equations for continuous model
• Support for general nonlinearities via collocation.
• Support for general sparse polynomial bases (perhaps better built into PolyChaos.jl, very awkward first attempt here)
• Support for algebraic models
• Support for stochastic optimal control problems (ControlSystems.jl)
• Support for multi-element PCE

@bowenszhu already contacted me and would like to help with some of the PCE efforts going forward as well, so it would be nice to get a pair of eyes on this as soon as possible.

Aside: Along the way of creating this, I found that working with PolyChaos.jl is extremely cumbersome. Among many things, the type structure underpinning PolyChaos.jl makes it particularly difficult to extend. For now I decided to work around that but we may wanna consider making changes to PolyChaos itself (I can go into more detail if we have any interest in that).

Flemming