ValueError: Parallel edges between H-boxes are not supported

[RDPEast]

I get the following error:

ValueError: Parallel edges between H-boxes are not supported

when trying to ZH simplify (' zx.hsimplify.hpivot_simp(spin, quiet=False) ') the following diagram encoded in JSON below:

spinjson = '{"wire_vertices": {"b0": {"annotation": {"boundary": true, "coord": [1.9, -0.7999999999999998], "input": true, "output": false}}, "b1": {"annotation": {"boundary": true, "coord": [2.25, -9.2], "input": true, "output": false}}, "b2": {"annotation": {"boundary": true, "coord": [21.9, -0.6000000000000001], "input": false, "output": true}}, "b3": {"annotation": {"boundary": true, "coord": [22.1, -10.9], "input": false, "output": true}}}, "node_vertices": {"v0": {"annotation": {"coord": [6.861683593750001, -0.8505781250000002]}, "data": {"type": "Z"}}, "v1": {"annotation": {"coord": [17.22468359375, -0.8204531250000002]}, "data": {"type": "Z"}}, "v2": {"annotation": {"coord": [5.988058593750001, -9.315703125]}, "data": {"type": "Z"}}, "v3": {"annotation": {"coord": [17.646433593750004, -9.767578125000002]}, "data": {"type": "Z"}}, "v4": {"annotation": {"coord": [8.187183593750001, -4.857203125000001]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v5": {"annotation": {"coord": [14.664058593750003, -4.827078125000001]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v6": {"annotation": {"coord": [18.941808593750004, -0.8505781250000002]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v7": {"annotation": {"coord": [4.029933593750001, -9.315703125]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v8": {"annotation": {"coord": [11.410558593750002, -1.8748281250000005]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v9": {"annotation": {"coord": [11.711808593750002, -7.387703125000002]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v10": {"annotation": {"coord": [11.832308593750001, -5.128328125000001]}, "data": {"type": "Z"}}, "v11": {"annotation": {"coord": [11.832308593750001, -9.225328125]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v12": {"annotation": {"coord": [11.320183593750002, -1.0614531250000003]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v13": {"annotation": {"coord": [6.379683593750001, -4.947578125000001]}, "data": {"type": "X", "value": "\\pi"}}, "v14": {"annotation": {"coord": [3.0358085937500006, -3.6823281250000006]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi/6"}}, "v15": {"annotation": {"coord": [3.1864335937500003, -5.459703125000001]}, "data": {"type": "hadamard", "is_edge": "false", "value": "11\\pi/6"}}, "v16": {"annotation": {"coord": [4.240808593750001, -4.3752031250000005]}, "data": {"type": "Z", "value": "\\pi/2"}}, "v17": {"annotation": {"coord": [1.9814335937500003, -4.525828125000001]}, "data": {"type": "X", "value": "\\pi"}}, "v18": {"annotation": {"coord": [4.542058593750001, -6.393578125000001]}, "data": {"type": "hadamard", "is_edge": "false", "value": "\\pi"}}, "v19": {"annotation": {"coord": [5.295183593750001, -8.201078125]}, "data": {"type": "Z"}}, "v20": {"annotation": {"coord": [4.240808593750001, -8.321578125000002]}, "data": {"type": "Z"}}, "v21": {"annotation": {"coord": [5.415683593750001, -6.092328125000002]}, "data": {"type": "X"}}}, "undir_edges": {"e0": {"src": "b0", "tgt": "v0"}, "e1": {"src": "b1", "tgt": "v7"}, "e2": {"src": "b2", "tgt": "v6"}, "e3": {"src": "b3", "tgt": "v3"}, "e4": {"src": "v0", "tgt": "v4"}, "e5": {"src": "v0", "tgt": "v8"}, "e6": {"src": "v0", "tgt": "v12"}, "e7": {"src": "v1", "tgt": "v6"}, "e8": {"src": "v1", "tgt": "v5"}, "e9": {"src": "v1", "tgt": "v8"}, "e10": {"src": "v1", "tgt": "v12"}, "e11": {"src": "v2", "tgt": "v7"}, "e12": {"src": "v2", "tgt": "v4"}, "e13": {"src": "v2", "tgt": "v9"}, "e14": {"src": "v2", "tgt": "v11"}, "e15": {"src": "v3", "tgt": "v5"}, "e16": {"src": "v3", "tgt": "v9"}, "e17": {"src": "v3", "tgt": "v11"}, "e18": {"src": "v10", "tgt": "v5"}, "e19": {"src": "v10", "tgt": "v4"}, "e20": {"src": "v10", "tgt": "v8"}, "e21": {"src": "v10", "tgt": "v9"}, "e22": {"src": "v10", "tgt": "v13"}, "e23": {"src": "v14", "tgt": "v17"}, "e24": {"src": "v14", "tgt": "v16"}, "e25": {"src": "v15", "tgt": "v17"}, "e26": {"src": "v15", "tgt": "v16"}, "e27": {"src": "v16", "tgt": "v13"}, "e28": {"src": "v16", "tgt": "v21"}, "e29": {"src": "v18", "tgt": "v20"}, "e30": {"src": "v18", "tgt": "v19"}, "e31": {"src": "v18", "tgt": "v21"}}}'

[jvdwetering]

Yeah there is no way in which to simplify multiple wires between H-boxes to a single wire, so the only way to deal with this is to keep all the edges around. But as pyzx only allows a single edge between vertices, we would have to introduce some dummy identity vertices. But then we would have to engineer smarter simplification strategies because you might otherwise get in an infinite loop. So I don't really know what a good solution to this is, other than changing all the simplification strategies to deal with this case.

[hmillerbakewell]

Does the following derivation (up to scalar) help you? It works with an number of parallel edges, not just two.

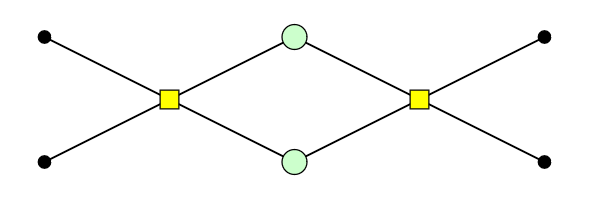
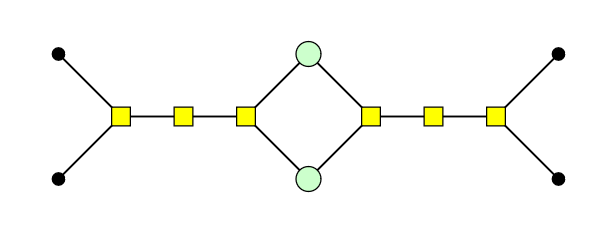
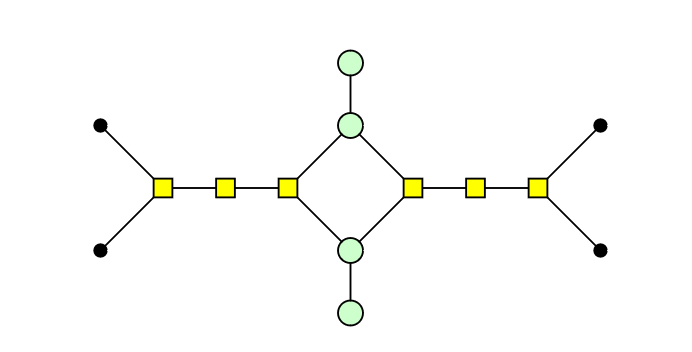
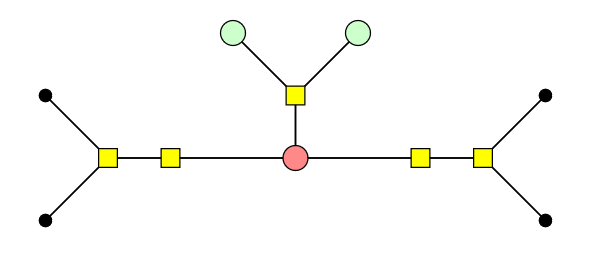
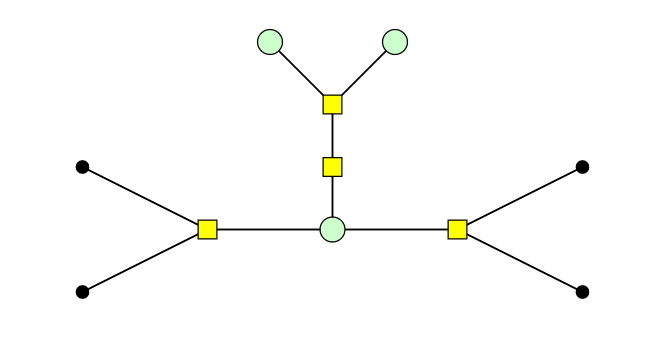
Any instance of multiple parallel edges can then be turned into a graph representable inside pyzx (that won't be immediately undone by the spider laws); whether this helps your simplification strategy is another matter.

[jvdwetering]

Hmm, yeah maybe I should let PyZX do this. I kinda need more examples to know what is the best thing to do in this case. And then there is of course also the issue of self-loops of H-boxes