Unknown Discretization and Oscillations of Articulation Body

[HA1N]

Hello Devs,

I have a problem using the Articulation Body Feature, which I used to implemented a Universal Robot 10 model in Unity. The end point of this robot should run a straight line when a predefined trajectory is applied. Due to gravity the end effector will lower as the arm moves further away from the base.

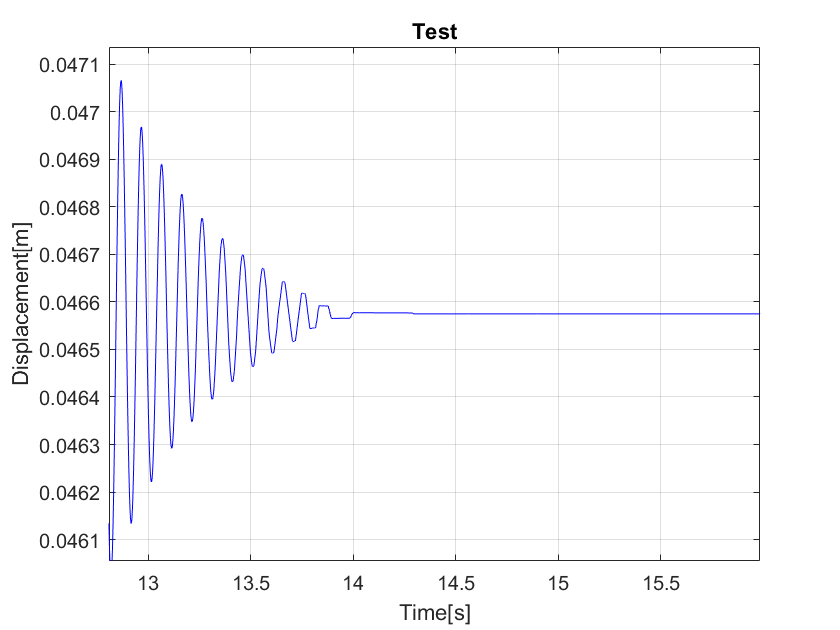
When the trajectory stops the robot oscillates until the final displacement of the end effector is reached (see Fig. 1).

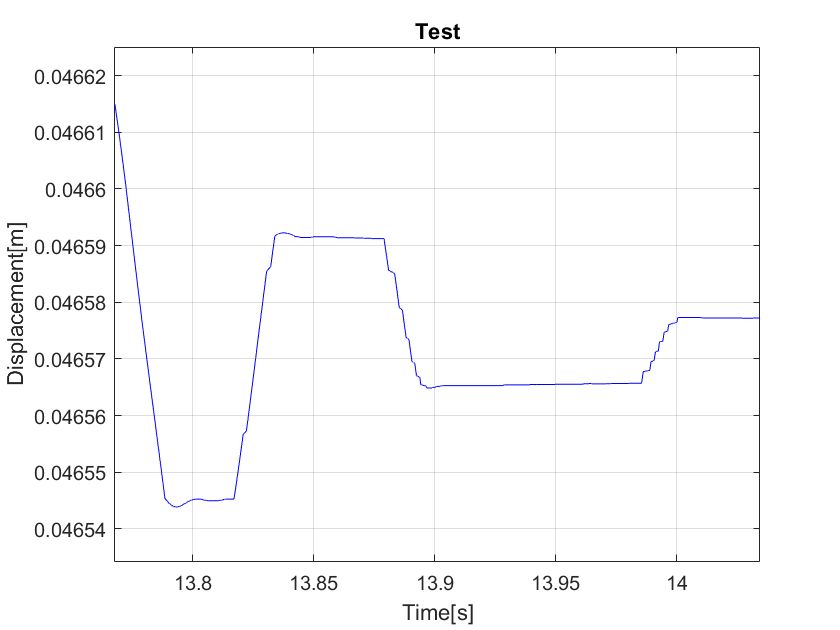
Taking a closer look shows some kind of discretization at the end of the run (See. Fig. 2).

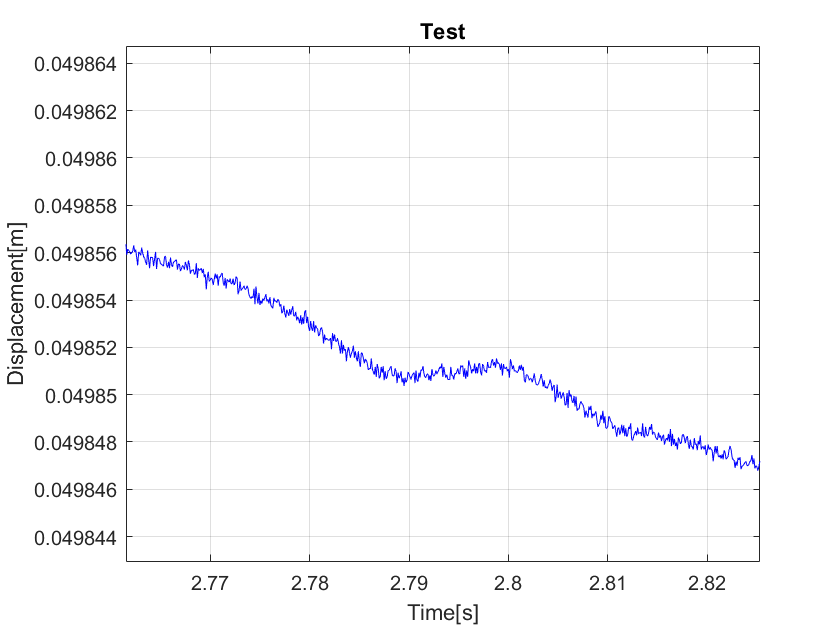
Observing the position of the end effector at an earlier time shows some unkown high frequency oscillations (see Fig. 3).

Please let me know whether this is a known behavior. Please let me know if you need more details about my implementation. Some speculations:

• The simulations runs for 20s at a timestep of 0.0001 s and the position of the end effector is monitored by a script. This could maybe cause the effect presented in Figure 2 because Unity can't compute every single timestep anymore.
• The trajectory sets the target angle of each joint each 0.001 s. The different timesteps of simulation and trajectory might cause the oscillations in Figure 3.

Thank you in advance!

Kind regards, Niklas

[kstorey-nvidia]

If you are using the built-in joint drives in the PhysX articulations, these are implemented as a PD controller.

If target joint angles are updated at a different frequency to the simulation, this could contribute to either discrete stepping or oscillation. If the stiffness is set high-enough, the PD controller will aggressively drive towards the target angle as quickly as possible rather than smoothly lerp to the target over the course of several frames. Depending on gain values, it is quite likely that it will overshoot and oscillate around the target. If this is undesirable, the damping term can be increased to cause the PD controller to undershoot rather than overshoot.

You may also be able to reduce oscillations by increasing the number of position iterations in the solver.

[HA1N]

Increasing the number of iteration numbers slightly decreased the the amplitude of the small oscillations. The damping value is taken from a reference model and should stay the same. The different update frequency of the target joint angles and simulation seem to be the main reason for the oscillations.

Regarding the first and second Figure: As it is shown in Fig. 1 the line is smooth at the beginning and starts to discretize around 13.75s. This problem is again shown in Fig. 2. Do you know any explanaition for this phenomenom?

[kstorey-nvidia]

This could be sleep related. Any simulated actor that reaches a rest state becomes a candidate for sleeping, where their simulation is disabled to improve performance.

You could try either setting the sleep threshold on the articulation links to be 0, or you could set the wake counter on the articulation to be some arbitrarily huge number. Setting the wake counter on the articulation to be something like 1e+20 would keep the articulation awake for a minimum of 1e+20 seconds.

[HA1N]

Thanks a lot for the helpful advice! Here are some new findings: After conducting new measurements the oscillations and discretizing don't seem to get better. The Figure shows the vertical displacement of the Tool-Center-Point (TCP) during a run. The robot arm is stretching so the TCP is lowering due to gravity.

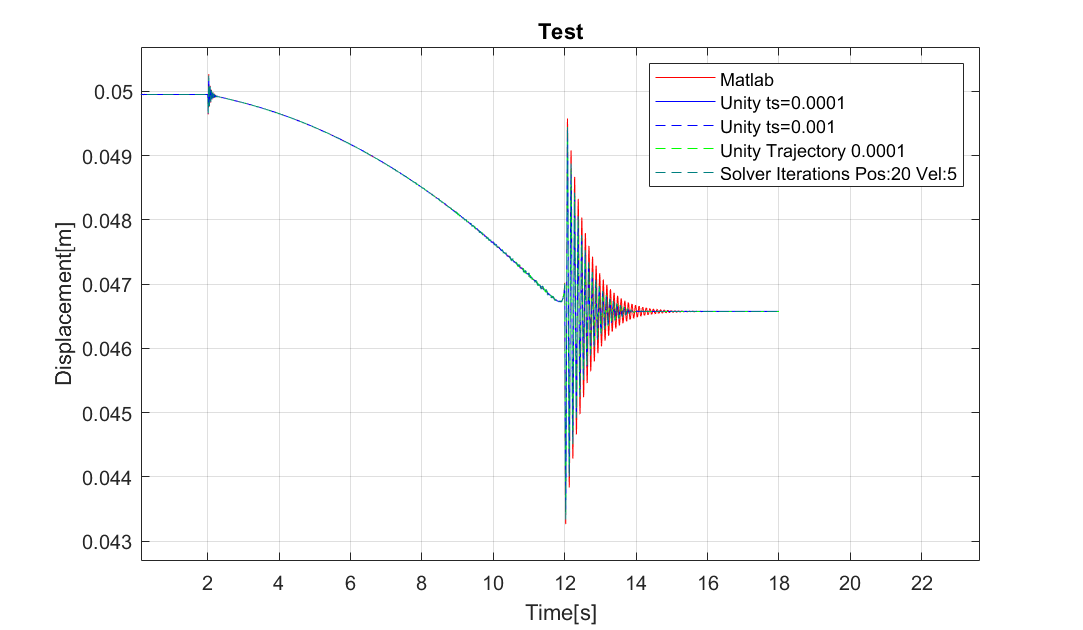
Zooming in on the area at around 11s is presented in the next Figure.

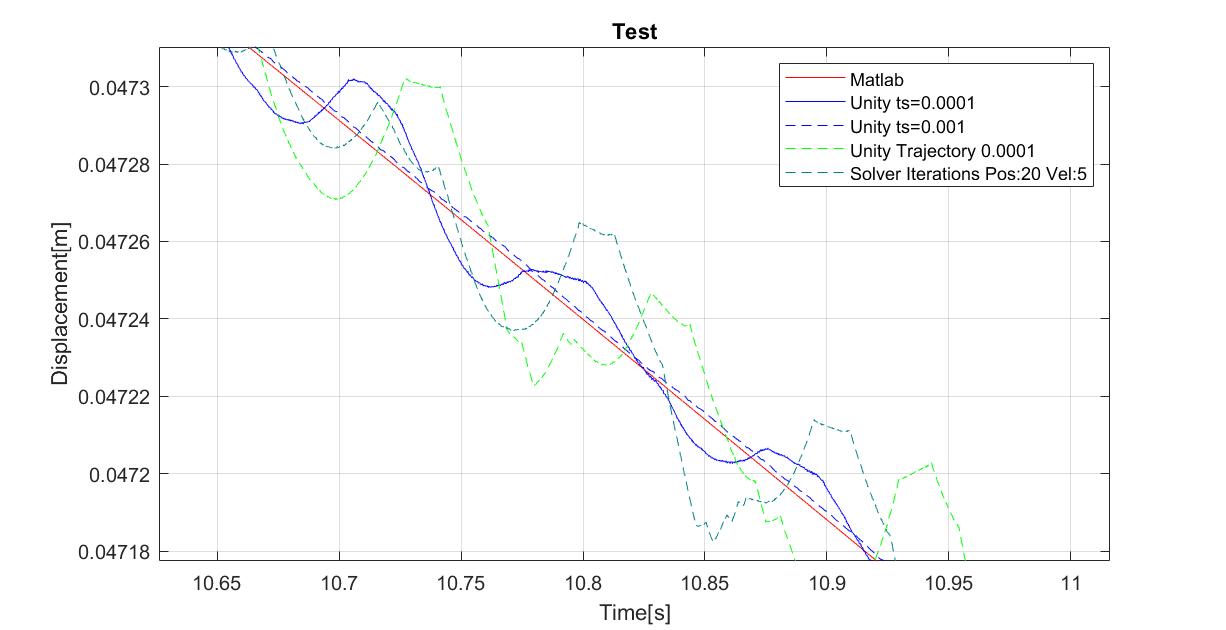
A short explanation of the different runs:

1. Matlab: Identical Matlab model that is used as a reference for the measurements taken with Unity
2. Unity ts=0.0001: Unity Simulation with timestep 0.0001s (Trajectory still has a timestep of 0.001s)
3. Unity ts=0.001: Unity Simulation with timestep 0.001s (Trajectory still has a timestep of 0.001s)
4. Unity Trajectory 0.0001: Simulation with new Trajectory timestep 0.0001s (Unity uses timestep 0.0001s as well)
5. Solver Iterations Pos:20 Vel:5 : Identical to previous case but higher solver iterations

As shown in the picture the 3. simulation gives the best approximation of the Matlab results. Because the timestep of simulation and trajectory were the same during this experiment I assumed a simulation using 0.0001s as a timestep for both would improve the results even further. Strangely enough the simulations using a smaller timestep (4.) as well as higher solver iterations (5.) result in worse approximations.

Regarding the discretization at the end of the runs: Modifying the "Sleep Threshold" and "Time To Sleep" settings didn't improve the results.