[Bug] Poromechanics problems with gravity do not produce expected stress field
Describe the bug I noticed some odd behavior in a model with poromechanics + gravity, so I put together a small test problem. In the example, I have a column of elements, with rollers on the +/-x, +/-y, and -z faces, and a constant pressure (0) on the z+ surface. The pressure and stress fields are initialized with values from a table (the python script used to build these is included).
The initial stress, pressure, and displacement in the model are:
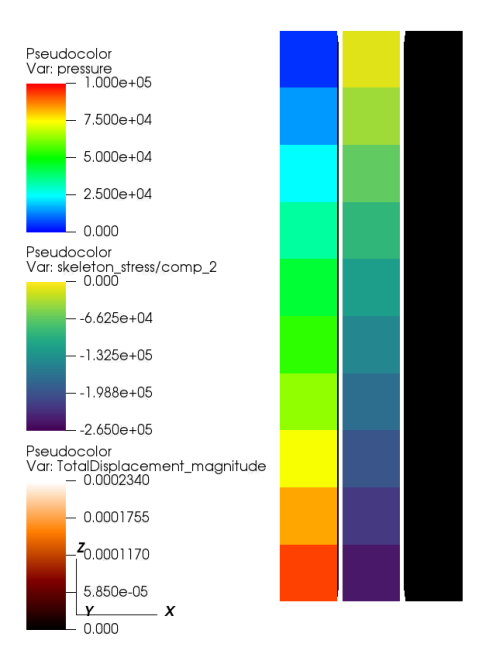
Applying either the solid mechanics or fluid solvers alone, yields correct looking results:
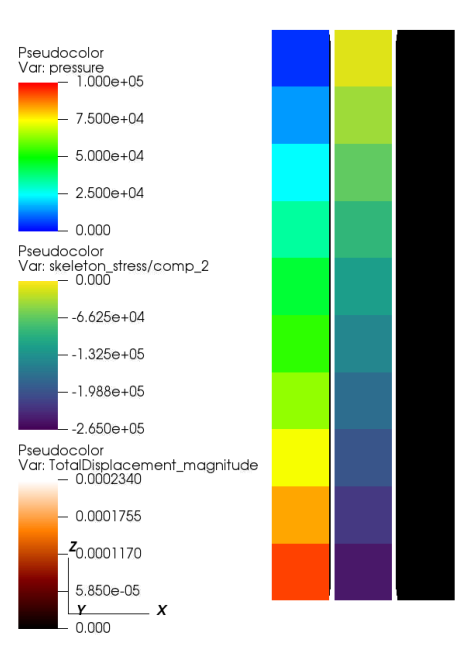
However, when the poroelastic solver is applied, the stress/displacement fields do not make sense:
To Reproduce
See the attached example here. In the event block, you can change which solvers are applied to the problem and see how the values change.
Hello @cssherman
There is a PR that fixes this issue: https://github.com/GEOSX/GEOSX/pull/1927
We have used it for our poromechanics field test cases with gravity, but I did not manage to merge it yet (mostly because the PR also does the initialization in a not so clean way). The PR changes the formulation of the body force terms and the density terms in the poromechanics solvers (single-phase and multiphase) to make sure that the stress and displacement are correct when you start the simulation with non-zero stress and pressure fields.
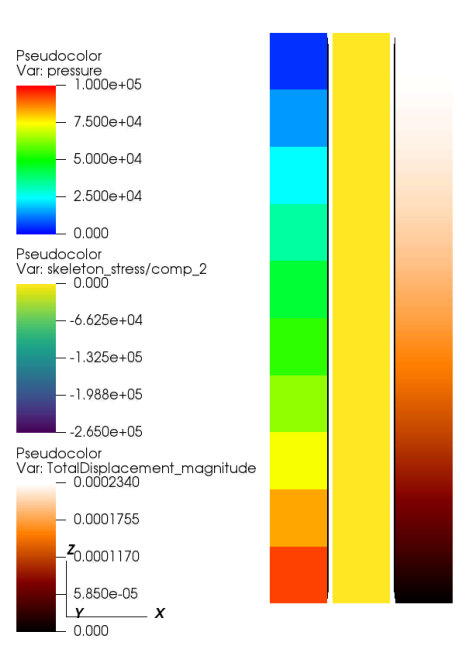
When I test the PR for your case with the two options (coupled, and elastic), it gives the correct results:
For elastic:
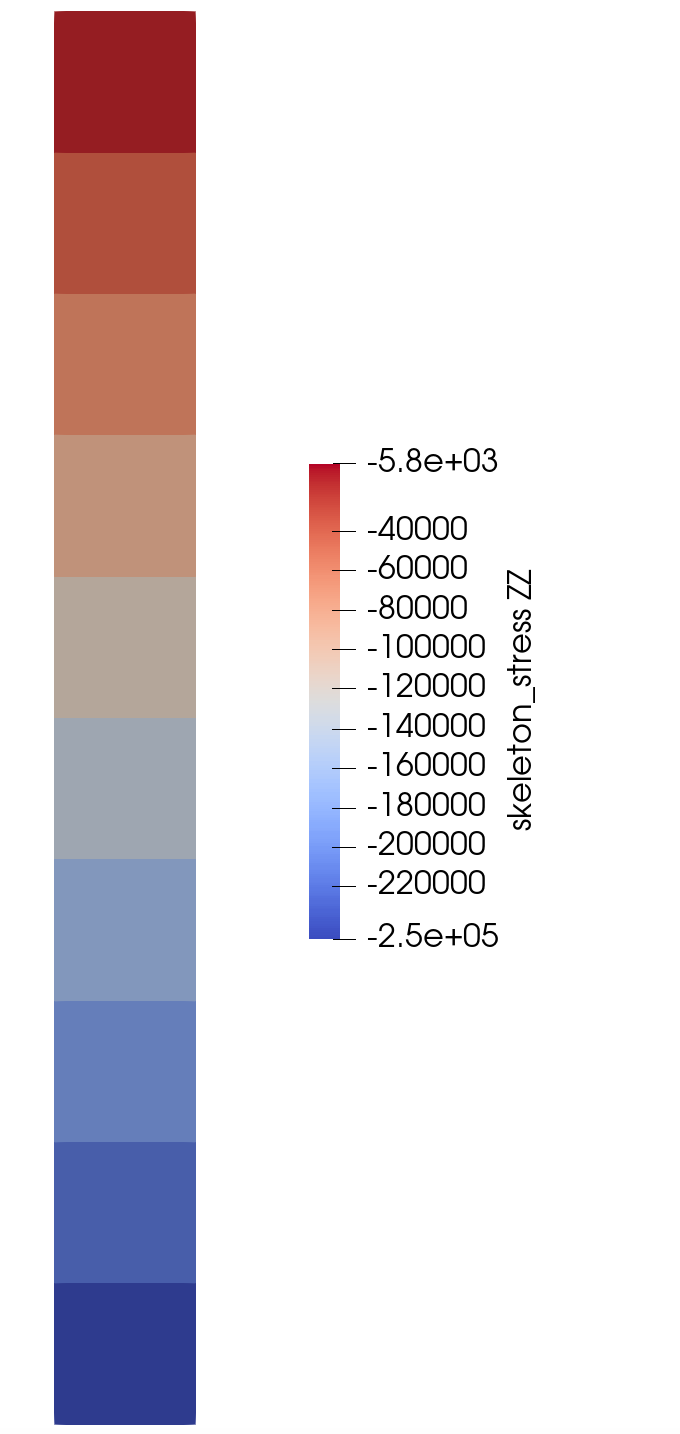
The domain is 10 meter long in the z direction. The rock density is 2600 kg/m^3. So I get a body force term of $\rho_{rock} \times g \times \Delta z = 255060$ Pa, which seems consistent with the stress value at the bottom of the model.
For coupled:
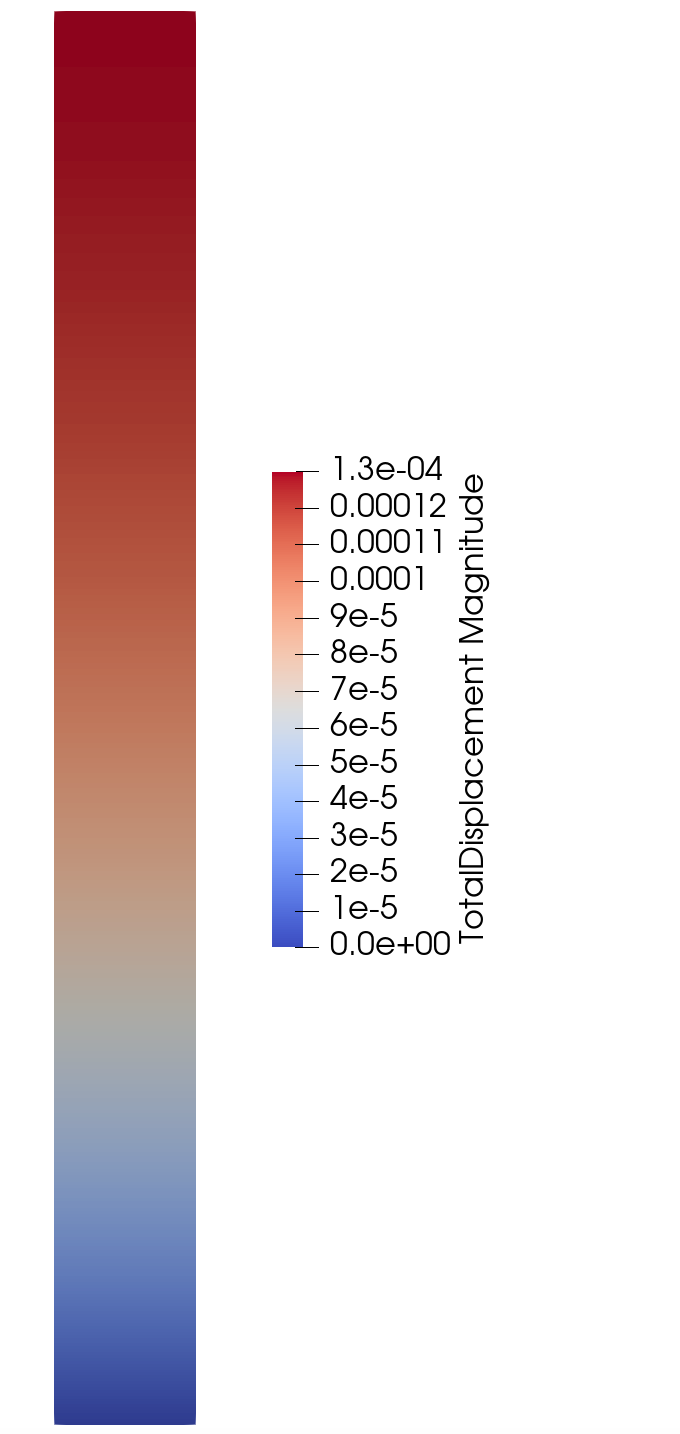
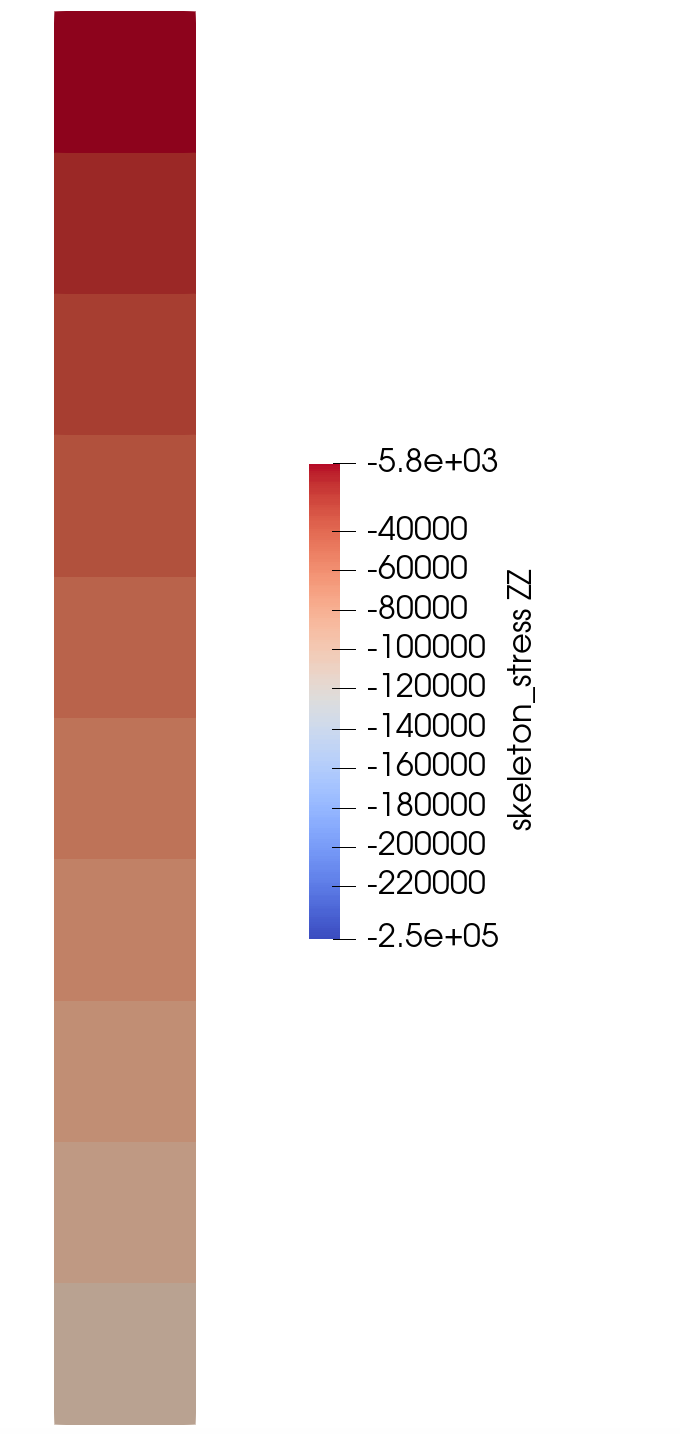
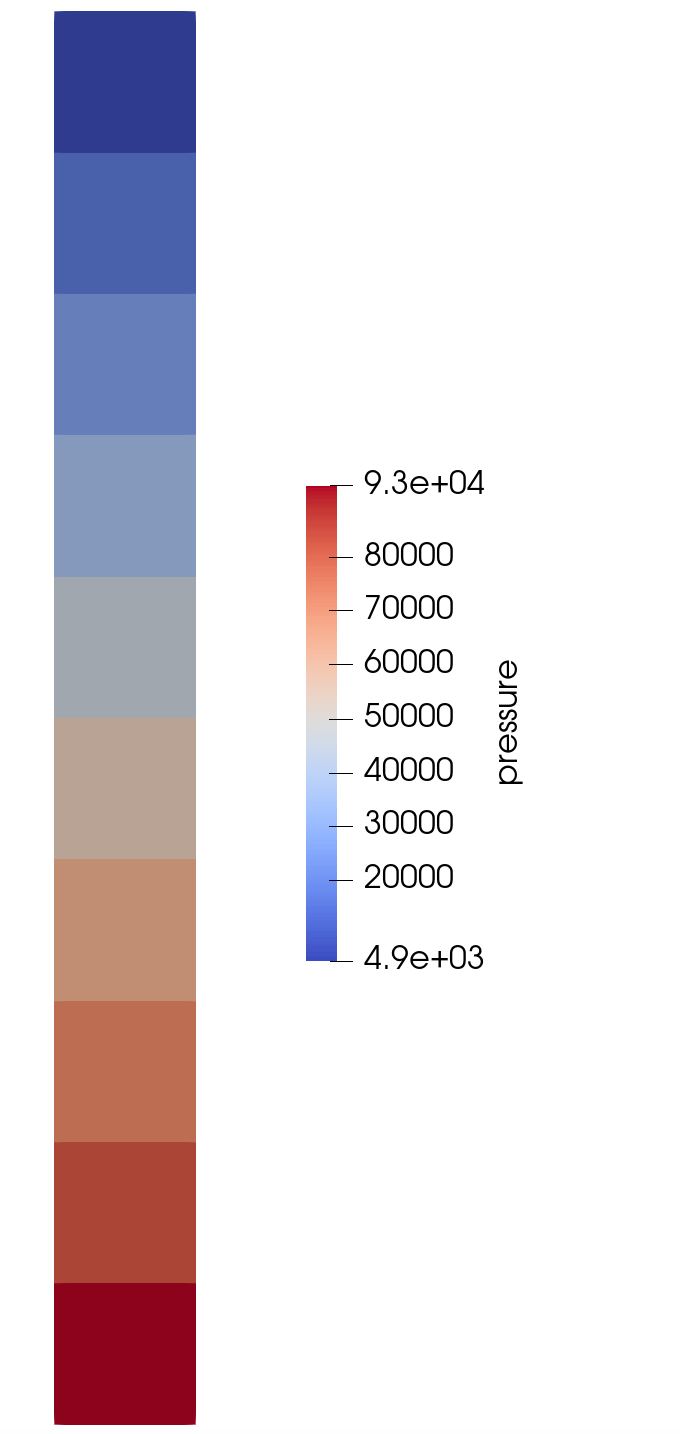
The domain is still 10 meter long in the z direction. The rock density is 2600 kg/m^3 and the fluid density is 1000 kg/m^3. The porosity is 0.3. So I get a body force term of $(\rho_{rock}(1-\Phi) + \rho_{fluid} \Phi ) \times g \times \Delta z = 207972$ Pa, which is in good agreement with the total stress (effective stress - pressure) that we obtain at the bottom of the domain.
I am going to fix this issue with a clean new PR if that is ok
Great, thanks!